10 a. Imaginary Boundaries

Solving a Different Problem

[Previously]

Let’s discuss spots some more, or dots this time, by looking at puzzle solutions. Here is The 9-Dot Problem again: “Draw no more than four straight lines (without lifting the pencil from the paper) which will cross through all nine dots.” (From Conceptual Blockbusting by James L. Adams)

Except where noted, the following solutions are from Conceptual Blockbusting.

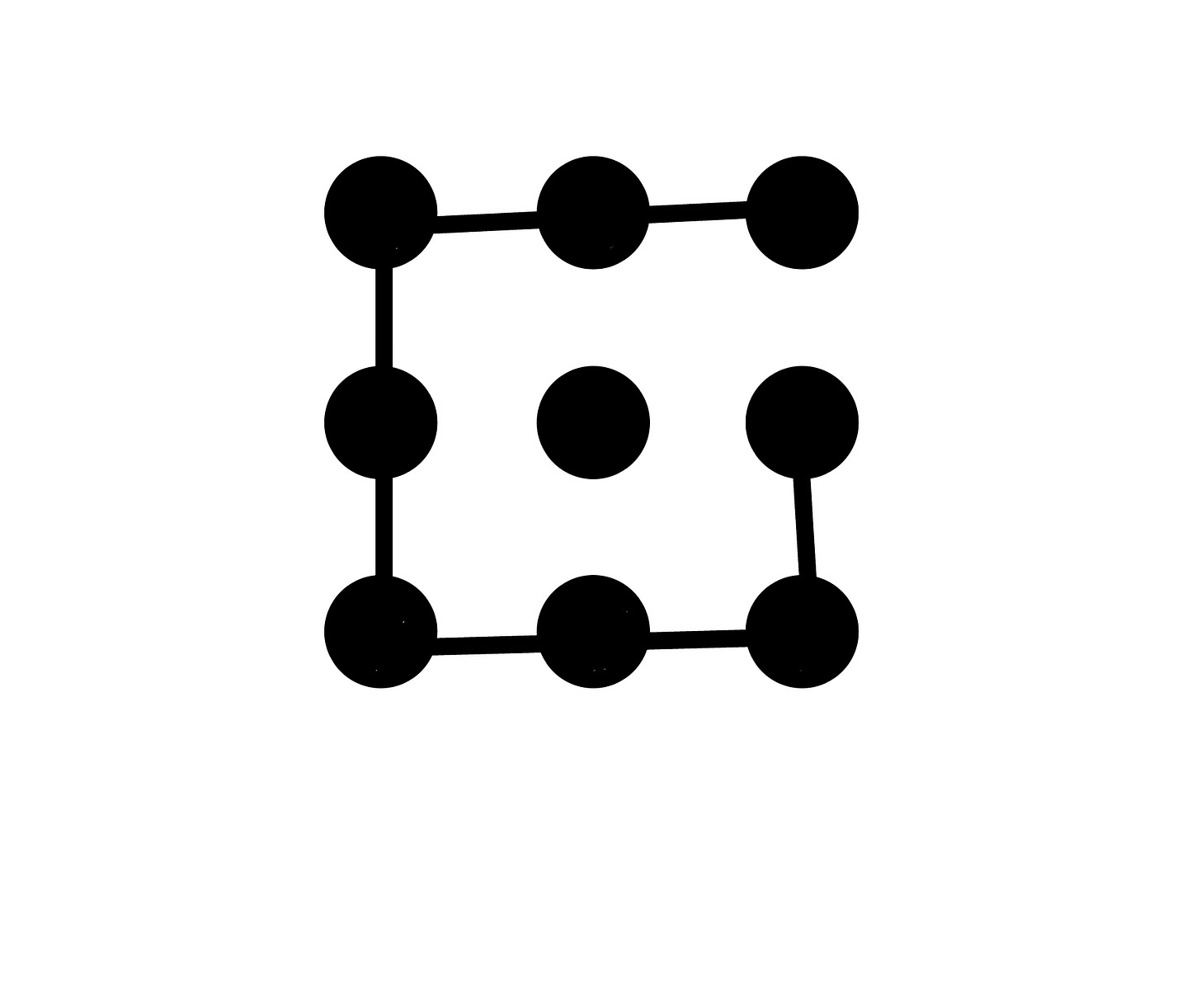
Not Possible

[An incomplete solution from class] For this problem solver, the puzzle can’t be solved. The dots make a square with one dot in the middle. Sure, you can draw four lines if you want—the problem is, you need five.

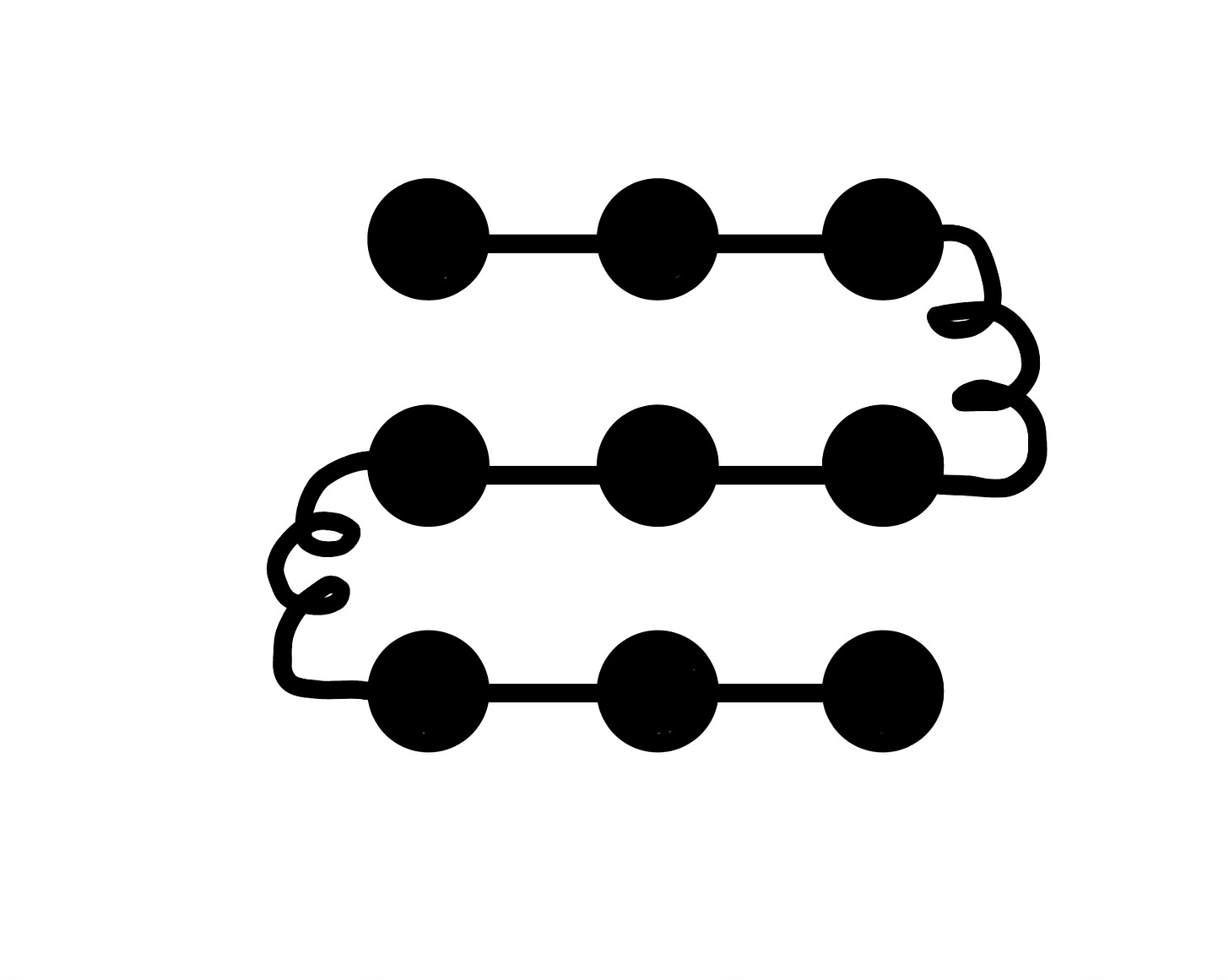
There’s Only So Much We Can Do

This solution, the most common one, causes debate. Some students say retracing is not ideal and it feels like cheating. The instructions say to “draw” no more than four straight lines but to do this solution, you need to draw six, even though only four are visible. “What is a line, though?” some ask. “No matter how many times you retrace, isn’t that still one line?” Even those who say this is a correct solution are not thrilled with it. It’s disappointing. Why did you waste our time with this? (The E solution can be an M or a W or a backwards E or, if you can retrace lines, why not go wild and make an asterisk?)

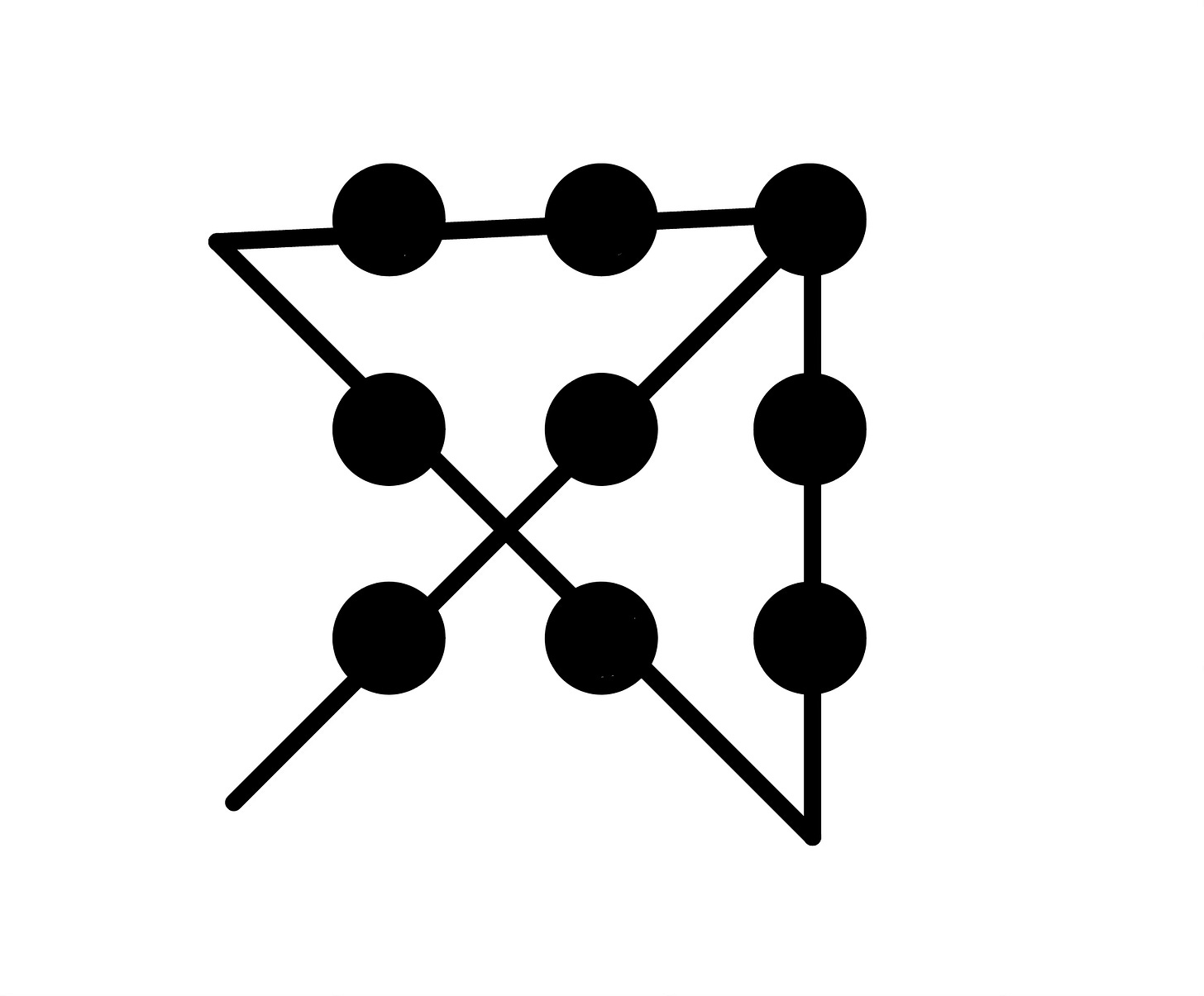
Why Didn’t I Think of That?

Usually, a few students come up with this arrow solution. Why not everyone? When most people look at the 9 dots, they see a square or a box, a boundary that you must stay within. Adams calls the square an “imaginary boundary.” The arrow problem solvers, however, believe there is no square hemming them in, even though it looks that way. There are only dots. Suddenly, what looks impossible is a piece of cake.

The Smart Aleck’s Answer

This one has only 3 straight lines, but it says no more than four, “So that’s okay,” says the smart aleck. “It doesn’t say anything about curves, right?” This solution was proposed by one of my students. It breaks imaginary boundaries not only by going outside the dots but also outside the lines.

A Child Shall Lead Them

This solution, done by a 9-year-old girl, disregards a couple of imaginary boundaries: the size of the dots and the thickness of the line. She drew the dots smaller and used a thick crayon when she drew her line.

Wrong Is the New Right

After I drew this on the chalkboard, my students said this solution is obviously false. It can’t be done without lifting the pencil.

“It’s correct,” I said.

“You lifted the chalk,” they said.

“No, I didn’t.”

“We saw you,” they said.

“Are you calling me a liar?” I asked.

“Yes,” they replied. “We are.”

I picked up a piece of paper and demonstrated the solution from Blockbusting. At first glance, the dots lie on a plane. But this problem solver knows that a plane does not have to stay that way. Forget your lame flat-world solutions. A plane can become a cylinder—just roll it up. With this new dimension, you can do more with less. The dots are easily connected. After you draw your line around your paper cylinder covering the dots as you go, just unroll the paper, and voila! A correct solution that appears impossible. Before, four lines were not enough; now, all you need is one (one line that is a curve, actually, until you flatten it out which then appears to be three unconnected lines). Why go back and forth when you can go 'round and 'round? Imaginary boundaries include dimensions. Why not take your two-dimensional problem and make it 3-D?

Endless Forms Most Beautiful

Adams has more solutions than I’ve included here, some of which involve scissors! Someone cut out the dots and stabbed the pencil, which served as a line, through all nine of them, creating a paper shishkabob. Students moaned about this one, claiming you can’t do that. “Okay then, so where in the instructions is your evidence that this violates the rules?”

This was always one of my favorite classes of the semester. Not only did it generate a lot of discussion, but you could see perspectives change before your eyes. Eventually, I asked, “Why do you think I’m spending so much time on a silly puzzle in a writing class?" After some discussion, they started to see a connection. “You don’t want us to limit ourselves,” they said.

In “The Cognition of Discovery: Defining a Rhetorical Problem,” Linda Flower and John R. Hayes say "good writers,” meaning the best of the writers in their study, which included students and professionals, “are simply solving a different problem" than “poor writers.” These writers get outside the dots by thinking about readers and their personal goals for the assignment instead of merely answering the question. They act like the “successful artists” from a study they cite (by Mihaly Cziksenthmihalyi) who “rearrange and play with alternatives” and “delay in reaching closure on the finished product.” These successful artist traits are handy for problem-solving and creativity, and good writers share these artists’ tactics. As we saw with the puzzle, how you envision the task is key. Is it possible as a writer to get outside the dots? Maybe it’s not only possible but required.

Adams claims imaginary boundaries, as demonstrated in his 9-dot problem, impede thinking and hinder creativity. He advocates “making the familiar strange”—looking at ordinary things from new perspectives, like our skateboarder and with the broccoli simile. Or, as we saw, the wrong metaphor can become one of these imaginary boundaries that can keep you trapped inside the dots and limit how you see things. When this happens, there are fewer possibilities. The puzzle solvers who came up with the arrow or the cylinder solutions, like the good writers, are not necessarily more intelligent. They were solving a different problem than the ones who stayed within the dots or kept the paper flat. Like the “poor writers” Flower and Hayes mention, the unsuccessful puzzle solvers are “not using skills they may well have.” Their “image of the problem” is what holds them back.

After these class sessions, the dots become a metaphor that helps students examine classmates’ essays. Did the writer get outside the dots? Are there places where they could do this but haven’t yet? They can also learn from classmates who escaped the dots or changed dimensions by studying the writer’s moves. What techniques, mindsets, and metaphorical concepts did they use that I could use, too?

What keeps some of us from using all the tools at our disposal, not just for puzzles or writing but in other aspects of our lives? Maybe breaking down imaginary boundaries is urgent, especially now.

Notes

Next, we’ll take a look at boundaries real and imaginary while discussing audience and genre.

If while doing your homework you came up with other solutions than seen here, feel free to post them in the comments.